

This is the same as the other hypotenuse because they are congruent sidesĪdd up all the sides to get 23.035 + 23.035 + 8 = 54. A triangle's height is the length of a perpendicular line segment originating on a side and intersecting the opposite angle. Plug that into your calculator to get that the hypotenuse is 23.035 Hence, the normal height ( Hn) of regular tetrahedron with edge length a is generalized by the formula. See our right triangle calculator to learn more about right triangles. Using the 80 degree angle, we can say that cos 80 = #(adj)/(hyp)# The normal height ( Hn) of any regular tetrahedron having edge length a is equal to the sum of radii of its inscribed & circumscribed spheres which is given as follows. The basic formula for triangle area is side a (base) times the height h, divided by 2: area (a × h) / 2 Height of the equilateral triangle is derived by splitting the equilateral triangle into two right triangles. We can use trigonometry to now find the hypotenuse of the small triangle. Much like the height of a book shelf can be measured, say 4 feet.

Since it acts as an angle bisector, the two vertex becomes two 10 degree angles.Ĭombine that with the fact that it is an altitude and we have formed two 10-80-90 triangles.Ĭombine that fact with the fact that it is a median and the base is bisected to a length of 4 for each of the smaller triangles. Equality () is used for measurements: length (inches, cm, etc.), angle measures (degrees), area (cm2). Since the triangle is isosceles, we can draw an altitude/angle bisector/median from the vertex angle down to the base. This isosceles triangle calculator can help with your geometry problems, finding area, height, angles, perimeter, or many other parameters.
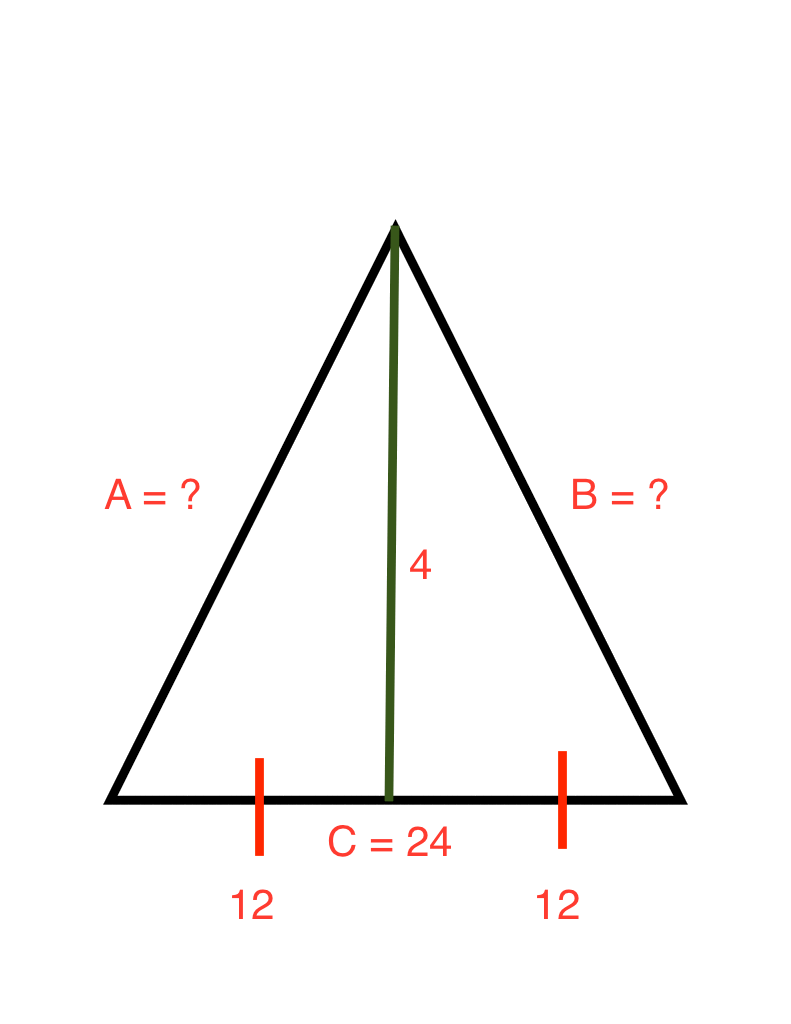
Since a triangle has 180 degrees and the vertex is 20, the 2 equal angles together are 160 degrees, thus each base angle is 80 degrees. Last, we calculate the area with the formula: 1/2 × base × height. Then we use the theorem to find the height. Once we recognize the triangle as isosceles, we divide it into congruent right triangles. I am not entirely sure of what you are allowed to use to answer this problem (presumably you can use a calculator because I did not find an easier way to answer this).įirst step is to find the base angles. We can find the area of an isosceles triangle using the Pythagorean theorem.


 0 kommentar(er)
0 kommentar(er)
